在概率论中，多臂老虎机问题是学习者必须在竞争性（alternative）选择之间分配固定的有限资源集，以最大化预期收益的问题。在此问题中，学习者仅部分了解每个选择的属性，随着“试验/游戏”轮次的增加及资源的逐步分配，他们对每个选择的了解越来越多。
这是经典的强化学习问题，它例证了勘探与开发之间的权衡困境。 想象在一排老虎机（有时称为“单臂匪徒”）前的赌徒，他们必须决定要玩哪些机器，每台机器玩多少次以及以什么顺序玩它们，是继续使用当前机器还是尝试其他机器。多臂老虎机问题也归入随机调度的大类里。
在问题中，每台机器根据其服从的特定概率分布提供随机奖励半岛体育娱乐。 赌徒的目标是通过一系列的pulls获得最大的累计奖励。赌徒在每次试验中面临着至关重要的tradeoff：对目前具有最高预期收益机器的“开发”VS对其他机器进行“探索”。 机器学习中也面临着探索与开发之间的权衡。 在实践中，多臂老虎机已被用来对一些问题建模，例如在大型组织（如科学基金会或制药公司）中管理研究项目。 在问题的早期版本中，t=0时赌徒对机器没有任何初步了解。
赫伯特·罗宾斯（Herbert Robbins）在1952年意识到问题的重要性，在“实验顺序设计的某些方面”构建了收敛的population选择策略。[6] 由John C. Gittins首次发布的一个定理，the Gittins index，为最大化期望折现报酬提供了一种最优策略。[7]
多臂老虎机问题模拟了一个代理，该代理同时尝试获取新知识（称为“探索”）并基于现有知识优化其决策（称为“探索”）。 代理试图平衡这些竞争性任务，以在一定时间内最大化其总价值。
强盗模型有许多实际应用，例如：
临床试验研究了不同实验方法的效果，最大程度地减少了患者的流失
自适应路由选择，可最大程度地减少网络中的延迟
金融投资组合设计
在这些实例中，问题需要在基于已经获取的知识的最大化奖励动作与尝试进一步增加知识的新动作之间取得平衡。 这被称为机器学习中的开发与探索权衡。（EE:exploration-exploitation tradeoff）
该模型还被用于控制对不同项目的资源动态分配，在不确定每种可能性的难度和回报的情况下，回答要从事哪个项目的问题。
最初由盟国科学家在第二次世界大战中考虑过，事实证明它是如此棘手，以至于彼得·惠特尔认为，the problem was proposed to be dropped overGermanyso that German scientists could also waste their time on it.
现在经常分析的问题版本由赫伯特·罗宾斯（Herbert Robbins）在1952年提出。
多臂老虎机MAB可以看作是一组实分布 
，第i杆奖励服从分布 
。 令 
是与这些奖励分布关联的平均值。
赌徒每轮反复play一个杆并观察相关的奖励。 目的是使所收集奖励总和最大化。 Horizon H是要播放的回合数。 老虎机问题在形式上等效于一个单状态的马尔可夫决策过程。T回合之后的遗憾 
定义为采用最佳策略时的奖励总和与所收集奖励总和之间的预期差：
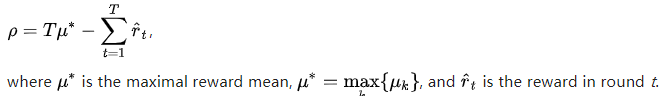
零后悔策略是指：当play的回合数趋于无穷大时，每回合的平均后悔
以概率1趋向于零。 凭直觉，如果进行了足够多的回合，则零后悔策略将被保证可以收敛于（不一定是唯一的）最优策略。
一种常见的表示形式是“Binary”或“伯努利”多臂老虎机，它们以概率p发出值为1的奖励，否则奖励为零。
多臂老虎机的另一种说法是，每个臂代表一台独立的马尔可夫机器。 每次play特定的手臂时，该机器的状态都会前进到根据Markov状态演化概率选择的新状态。 根据机器的当前状态产生相应奖励。 在一种被称为“restless老虎机问题”的概括中，未使用的臂的状态也会随时间演化。[15] 还讨论了系统的选择（随着时间的推移，选择哪个手臂）随时间增加的情况。[16]
计算机科学研究人员研究了最坏情况下的多臂匪徒，获得了不同算法以最大程度减少随机[1]和非随机[17]手臂收益的有限和无限（渐近）时间范围内的遗憾。
在论文“渐近有效的自适应分配规则Asymptotically efficient adaptive allocation rules”中，Lai和Robbins [18]（Robbins及其同事在1952年回到Robbins的论文之后）对population奖励分布是单参数指数族的情况。构建了收敛的population选择策略，该策略具有最快的收敛速度（收敛至(the population with highest mean)）。然后，Katehakis和Robbins在 [19]中，对于具有已知方差的正常population，简化了政策并提供了主要证明。 Burnetas和Katehakis在论文“针对顺序分配问题的最佳自适应策略Optimal adaptive policies for sequential allocation problems” [20]中获得了下一个显著进展，其在更普遍的条件（包括分布情况）下构造了具有一致最大收敛速度的基于index的策略。每个population的结局取决于未知参数的向量。另外，他们还为一种重要情境（在这种情境下，outcomes服从任意（i.e.非参数）离散的单变量分布）提供了一个明确的解决方案。
之后，在“马尔可夫决策过程的最佳自适应策略Optimal adaptive policies for Markov decision processes” [21]中，Burnetas和Katehakis研究了部分信息下的马尔可夫决策过程的更大模型，其中过渡律和/或预期的一阶段（one period）回报可能取决于未知参数。在有限的状态-作用空间和过渡律的不可约性的充分假设下，这项工作构造了对总的有限轮次期望回报具有一致最大收敛速率的一系列自适应性策略的显式形式。这些政策的主要特征是，在每个状态和时间段内，对行动的选择均基于index，第i臂的index是第i臂的实际平均奖励与一乐观估计项之和。 这些不同类型的乐观估计项最近在Tewari和Bartlett [22] Ortner [23] Filippi，Cappé和Garivier [24]以及Honda和Takemura的工作中被称为乐观方法。[25]
老虎机问题存在许多求解策略，它们可以提供一个近似的解决方案，并且可以分为以下四大类。
Semi-uniform strategies
Semi-uniform strategies是最早（且最简单）的策略，可用来近似解决老虎机问题。 所有这些策略都有一个贪婪的行为：除非采取（一致的）随机动作，否则总是会（基于先前的观察）拉动最佳杠杆。
a.Epsilon-greedy策略：学习者以 
的概率选择最佳臂，以 
的概率随机选择一个臂。 通常取0.1，它可根据情况和偏好而vary widely。
b.Epsilon优先策略：在纯勘探阶段之后是纯exploitation阶段。对于总的N轮试验，探索阶段占用 N轮，而exploitation则占 
N轮。在探索阶段，随机选择一个臂（概率均匀）。在exploitation阶段，始终选择最佳杠杆。
c.Epsilon减少策略：与epsilon-greedy策略类似，不同之处在于 的值会随着实验的进行而降低，从而在开始时产生高度探索性的行为，而在接近结束时高度exploitation。
d.基于价值差异的自适应epsilon贪婪策略（VDBE）：与epsilon减少策略类似，不同之处在于此处epsilon是根据学习进度而不是手动调整减少的（Tokic，2010年）。[27]价值估算的高波动导致高ε（高exploration，低exploitation）；低波动导致低ε（低exploration，高exploitation）。对于探索性选择，可以通过选择softmax加权来实现进一步的改进（Tokic和Palm，2011年）。[28]
e.Contextual-Epsilon-greedy策略：与epsilon-greedy策略类似，不同之处在于根据实验过程中的situation计算 的值，这使该算法是Context-Aware的。它基于动态exploration-exploitation，可以通过确定哪种情况与exploration或exploitation最相关来自适应地平衡这两个方面，从而在非关键情况下产生高exploration的行为，在关键情况下产生高exploitation的行为。[29]
概率匹配策略
概率匹配策略反映了这样一种思想，即给定臂的拉动次数应与其作为最佳臂的实际概率相匹配。概率匹配策略也被称为汤普森采样或贝叶斯老虎机[30]，如果您可以从后验取每个备选方案的均值，那么该方法将很容易实现。
概率匹配策略也允许解决所谓的上下文Contextual 老虎机问题。
定价策略
定价策略确定每个臂的价格。例如，如POKER算法所示，[14]价格可以是预期奖励与通过额外知识获得的额外未来奖励的估计之和。最高价格的臂始终被拉动。
有道德约束的策略
这些策略最小化了将任何患者归属到inferior臂的分配（“医师的职责”）。在典型情况下，它们使预期的成功损失（ESL:将资源错配给inferior臂而没有获得最优臂奖励的损失）。另一种版本则将浪费在劣等、更昂贵的治疗上的资源减至最少。[8]
多臂老虎机的一个特别有用的版本是上下文多臂老虎机问题。在这个问题中，代理（学习者）必须在每次迭代之间进行选择。在做出选择之前，代理会看到与当前迭代关联的d维特征向量（上下文向量）。学习者使用这些上下文向量以及过去玩过的臂的奖励来选择要在当前迭代中玩的臂。随着时间的推移，学习者的目标是收集有关上下文向量和奖励如何相互关联的充足信息，以便它可以通过查看feature向量来预测下一个最佳手臂。[31]
Contextual bandit的近似解决方案
有许多策略可以为Contextual bandit问题提供近似解决方案，并且可以分为以下两大类。
1)在线线性分类器
LinUCB（Upper Confidence Bound）算法：作者假设动作的预期奖励与其上下文之间存在线性相关性，并使用一组线性预测变量对表示空间进行建模。
LinRel(Linear Associative Reinforcement Learning)算法：与LinUCB相似，但利用奇异值分解而非Ridge回归来获得更好的置信度估计。[32] [33]
2)在线非线性分类器
UCBogram算法：在非参数回归中，使用称为“回归图”的分段常数估算器估算非线性回报函数。然后，在每个恒定块上使用UCB。上下文空间分区的连续优化 are scheduled or chosen adaptively.
NeuralBandit算法：该算法训练了多个神经网络，以在知道上下文的情况下对奖励的值进行建模，并使用多专家方法在线选择多层感知器的参数。[37]
KernelUCB算法：一种线性化的LinearUCB非线性版本，具有高效的实现和有限时间分析的功能。[38]
bandit Forest算法：建立并分析随机森林，而无需了解上下文和奖励的联合分布即可建立随机森林。[39]
在实践中，通常存在与每个操作消耗的资源相关的成本，并且在诸如众包和临床试验等许多应用中，总成本受到预算的限制。约束上下文强盗（CCB）是一种在多臂老虎机设置中同时考虑时间和预算约束的模型。 A. Badanidiyuru等人[40]首先研究了有预算约束的Contextual bandit，也称为Resourceful Contextual bandit，并证明了O( 
) 后悔是可以实现的。但是，他们的工作集中在一组有限的策略上，并且该算法在计算上效率低下。
[41]提出了一种具有对数后悔的简单算法：
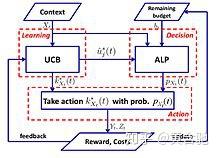
UCB-ALP算法：下图显示了UCB-ALP的框架。 UCB-ALP是一种简单的算法，将UCB方法与自适应线性规划（ALP）算法结合在一起，可以轻松地部署到实际系统中。这是第一部展示如何在受限的Contextual bandit中实现对数后悔的工作。尽管[41]专门针对单一预算约束和固定成本的特殊情况，但结果为更一般的CCB问题的算法设计和分析提供了启示。
多臂老虎机问题的另一种形式为对抗性老虎机，它由Auer和Cesa-Bianchi（1998）首先提出。在此变体中，每次迭代时，代理人选择一个臂，而对手同时为每个臂选择payoff结构。这是老虎机问题的最强概括[42]，因为它消除了所有分布假设，而且对抗性老虎机问题的解决方案是更具体老虎机问题的广义解决方案。
例子：iterated 囚徒困境
对抗性老虎机经常考虑的一个例子是囚徒困境。在此例中，每个对手都有两个要拉的手臂。他们可以拒绝也可以坦白。标准随机bandit算法在此迭代中效果不佳。例如，如果对手在前100轮中合作，在接下来的200轮中出现缺陷(defects)，然后在接下来的300轮中合作，以此类推。那么诸如UCB之类的算法将无法对这些变化做出非常迅速的反应。这是因为在某个点之后，很少会抽出次优臂来限制exploitation并专注于exploration。当环境变化时，算法将无法适应甚至无法检测到变化。
exp3算法
Exp3随机选择概率为 
的手臂，它更喜欢权重较高的手臂（exploit），以γ的概率均匀地随机探索。 收到奖励后，权重将更新。 指数增长显着增加了良好臂的权重。
Exp3算法的external后悔最多为 
.
Follow the perturbed leader (FPL) 算法
我们沿用了迄今为止我们认为具有最佳性能的手臂，为其添加了指数噪声以提供探索。[44]
Exp3 vs FPL
Exp3： FPL：
保持(Maintains)每个臂的权重以计算pull的概率 不需要知道每条臂的pull概率
有有效的理论保证 标准FPL没有良好的理论保证
在计算上可能会很昂贵（计算指数项） 计算相当efficient
无限臂老虎机
在原始规范和上述变体中，匪徒问题是通过离散且数量有限的臂来指定的，通常由变量{\ displaystyle K} K表示。在Agarwal（1995）提出的无限武装的情况下，“武器”是{\ displaystyle K} K维度上的连续变量。
非平稳老虎机
Garivier和Moulines得出了一些有关匪徒问题的第一批结果，这些问题的基本模型可以在比赛中改变。提出了许多算法来处理这种情况，包括贴现UCB [45]和滑动窗口UCB [46]。
Burtini等人的另一项工作。引入了加权最小二乘汤普森采样方法（WLS-TS），在已知和未知的非平稳情况下都证明是有益的。[47]在已知的非平稳情况下，[48]中的作者提出了另一种解决方案，即UCB的一种变体，称为“可调整的上限置信区间”（A-UCB），它采用了随机模型并提供了遗憾的上限。
其他变形
近年来，已经提出了该问题的许多变体。
1.Dueling 老虎机
Dueling老虎机由Yue等人引入。 （2012）[49]建模E-E tradeoff的相对反馈。在此变体中，赌徒被允许同时拉两个臂，但是他们只能得到binary反馈，告诉哪个臂提供了最好的回报。这个问题的困难源于以下事实：赌徒无法直接观察其行为的回报。解决此问题的最早算法是InterleaveFiltering，[49] Beat-The-Mean。[50]。Dueling老虎机的相对反馈也会导致投票悖论。一种解决方案是以Condorcet获奖者作为参考的。[51]
最近，研究人员已将算法从传统的MAB推广到Dueling bandits：相对上限置信区间（RUCB），[52]相对指数加权（REX3），[53]Copeland置信区间（CCB），[54]相对最小经验散度（ RMED），[55]和双重汤普森采样（DTS）。[56]
2.协作老虎机
Li和Karatzoglou和Gentile（SIGIR 2016）引入了协同过滤；老虎机（即COFIBA）[57]，其中经典的协同过滤和基于内容的过滤方法试图在给定训练数据的情况下学习静态推荐模型。这些方法在诸如新闻推荐和计算广告之类的高度动态的推荐领域中远非理想，在这些领域中项目和用户的流动性非常强半岛体育娱乐欢迎您。在这项工作中，他们研究了一种Contextual bandit环境中基于E-E策略的内容推荐自适应聚类技术。[58]他们的算法（COFIBA，发音为“ Coffee Bar”）考虑到了用户与商品互动所产生的协同效应[57]，它是根据考虑中的商品动态对用户进行分组，同时，根据在用户上引起的聚类相似性对项目进行分组。因此，所得算法以类似于协作过滤方法的方式利用了数据中的偏好模式。他们提供了对中型现实世界数据集的实证分析，显示了可伸缩性和增强的预测性能（通过点击率衡量），优于最新的集群bandits方法。它们还在标准线性随机噪声设置内提供了遗憾分析。
3.组合老虎机乐虎平台
当代理人需要为一组变量选择值而不是从中选择一个离散变量时，就会出现组合多臂老虎机（CMAB）问题[59] [60] [61]。假设每个变量都是离散的，则每次迭代的可能选择数与变量数成指数关系。文献中已经研究了几种CMAB设置，从变量是binary的设置[60]到更通用的设置，每个变量可以采用任意值集。[61]
四虎影院最新网址更新四虎影院在线观看
参考资料：https://en.wikipedia.org/wiki/Multi-armed_bandit#cite_note-GLZ2014CLUB-58 四虎github
